EJERCICIOS
Se dice que una funcion f(x), es periodica con periodo T > 0, si se cumple que:
f (x + t) = f (x) para todo valor de x, en el cual se encuentra en el dominio de la funcion F (x).
1. f(x) = cos(x), 0 <= x <= 2pi T = 2pi
cos (0) = cos(0+2pi)
cos(0) = cos(2pi)
cos(0) = cos(360)
2. f(x) = sin 2x , o <= x <= 2pi
2pi/2 = pi
3. f(x) = cos(x+4pi), 0 <= x <= 2pi
= 2pi
4. f(x) = sin x + 1/2 sin(2x) +1/3 sin(3x) + 1/4 sin(4x), 0 <= x <= 2pi
periodicidad de sin(x) = 2pi
periodicidad de 1/2 sin(2x) = pi
periodicidad de 1/3 sin(3x) = 2pi/3
periodicidad de 1/4 sin(4x) = pi/2
combinar periodos: 2pi, pi, 2pi/3, pi/2
= 2pi
Evaluar las siguientes integrales
1.
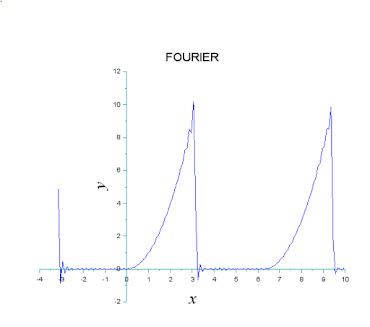
Se evaluara las siguientes integrales y así mismo se evaluara en el software de Scilab y Desmos.
La solución es:









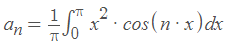
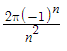







Comentarios
Publicar un comentario